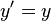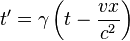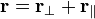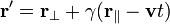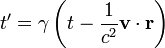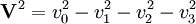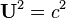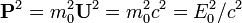Ara
Webde Aradığınız Herşey
ozel gorelilik kurami izafiyet teorisi
Genel
Galilei'ye göre sabit hızla giden bir gözlemci veya sabit duran gözlemci aynı fiziksel yasaları kullanmalıdır. Örneğin sabit hızla giden bir gemide yukarı doğru bir taş atarsanız aynı yere düşecektir - sabit durduğunuzda olduğu gibi. Bu anlayış Newton fiziğinde formülasyona dökülmüştür. Sabit hızla giden bir cisim veya sabit duran bir cisim için geçerli olan Newton denklemlerinin şekli aynıdır. Burada şunu belirtmekte fayda var. Sabit hızla giden bir cisim gözlemciye göre tanımlanmaktadır. Eğer bir cisimle beraber aynı sabit hızla gidiyorsanız sizin için cisim hareketsiz görünecektir. Fakat dışarıdan bakan bir gözlemci için cisim hareketli kabul edilir. Görelilik kelimesi burada ortaya çıkmaktadır. Bizim gözlemlediğimiz hızlar mutlak değildir. Ancak gözlemciye göre tanımlanmaktadır. Ama gözlemlenen olay için geçerli olan yasaların şekli aynıdır.
Sabit hızla giden (ivmelenmeyen) referans sistemlerine eylemsiz referans sistemi denir. Bu kavramın özel görelilik kuramında çok önemli bir yeri vardır. Özel görelilik kuramına göre hiç bir eylemsiz referans sisteminin bir diğerine bir üstünlüğü yoktur ve hepsinde yapılan gözlemler aynı derecede geçerlidir.
Düzgün-doğrusal hareketli cisimlerin elektrodinamiğinde Einsten şunları keşfetmişti:
- Bizler 3 uzay ve 1 zaman boyutunun meydana getirdiği, 4 boyutlu uzay-zaman evreninde yaşıyoruz.
- Zaman boyutu ve akışı, hareketli cisimlerin hızına bağlıdır.
- Kütle, hareketli cisimlerin hızına bağlıdır.
- Cismin hareket doğrultusundaki boyu, cismin hızına bağlıdır.
- 4 boyutlu evrende "aynı anda olma" kavramı da mutlak değildir, görelidir, yani aynı andalık gözlemciden gözlemciye değişir.
- Farklı hızda hareket eden cisimlerin uzay-zaman referansları birbirinden farklıdır.
- Işık hızı evrendeki üst hız limitidir.
Özel görelilik kuramının gücü ve sağlamlığının en önemli nedeni,sadece iki kabullenim (postulate)üzerine inşa edilmiş olmasıdır. Bu kabullenimler:
- Fizik yasaları evrenin her yerinde ve bütün eylemsiz referans sistemlerinde aynı şekilde işler.(Bu kabüllenim evrensel bir referans sitemin yokluğundan kaynaklanmaktadır.Eğer fizik yasaları birbirine göre bağıl harekette bulunan farklı gözlemcilere göre farklı olsalardı ;gözlemciler,bu farklılıkları kullanarak uzayda hangisinin "durgun",hangisinin "hareketli" olduklarını bulabilirlerdi.Fakat böyle bir farklılık yoktur ve görelilik ilkesi bu gerçeğin ifadesidir.)
- Işığın hızı, bütün eylemsiz referans sistemlerinde aynı ve sabittir.
Kuramın temel aldığı bu iki kabullenimden biri çürütülemediği sürece kuram doğruluğunu koruyacaktır.
Öngörüleri
Özel görelilik, kendi zamanı için inanılması güç pek çok öngörülerde bulunmuştur, bunlardan en önemlileri:
- Cisimler hızlandıkça zaman cisim için daha yavaş akmaya başlayacaktır, ışık hızına ulaşıldığında zaman durmalıdır.
- Cisimler hızlandıkça kinetik enerjilerinin bir kısmı kütleye dönuşür, durağan kütleye sahip cisimler hiçbir zaman ışık hızına erişemeyeceklerdir.
- Cisimler hızlandıkça hareket doğrultusundaki boyları kısalmaya uğrayacaktır.
Özel görelilik, mantığımıza ve sağ duyumuza aykırı bir evren tanımladığından bilimciler 100 yılı aşkın bir süredir bunun doğruluğunu gözleri ile görmek ve bir açık bulmak umudu ile deneyler yapıp durmaktadırlar. Bu öngörülerin pek çoğu 1905'dan günümüze dek defalarca denenmiş ve doğru çıkmıştır:
- İçlerinde çok hassas atom saatleri taşıyan uçaklar değişik yönlere doğru değişik hızlarla hareket ettirilmiş ve saatlerin kuramın hesaplarına yeterince uygun olarak yavaşladığı/hızlandığı gözlenmiştir[1].
- Zamandaki yavaşlamanın sadece saatte meydana gelmediğini, gerçekte yaşandığının kanıtı ilk olarak nötrino ve mü-mezon deneylerinde ortaya çıkmıştır. Güneşten dünyamıza gelen nötrino ve müonların ışık hızına çok yaklaştıkları (%99.5) için ömürlerinin (yaşam sürelerinin) Dünya'da üretilen durağan olanlara göre çok daha uzun olduğu görülmektedir[2].
- Parçacık hızlandırıcılarındaki hızlandırma deneylerinde bugüne kadar kütlesi olan hiçbir cisim, atom veya elektron, ışık hızına çıkarılamamıştır. Hız arttıkça kütlesi de arttığı için ivmelendirilmesi zorlaşmaktadır.
Galilie ve Lorentz dönüşümleri
- Ana madde: Lorentz dönüşümleri
Değişik gözlemciler Newton fiziğinde Galile dönüşümleri tarafından tanımlanmaktadır. Öncelikle belirli bir O olayı için (x,y,z,t) koordinatlarını kullanan bir R1 referans sistemi düşünelim. Aynı olayın başka bir gözlemci tarafından (x',y',z',t') koordinatlarıyla ifade edildiğini farz edelim (R2 referans sistemi). Eğer R2, R1 sistemine göre sabit bir hızla x ekseninde hareket ediyorsa gözlemlenen O için kullanacakları referans sistemleri arasındaki bağıntı şöyle olacaktır:
- x' = x − vt
- y' = y
- z' = z
- t' = t

Bu dönüşümler Newton'un mekanik yasalarına uygulandığında, yasalar formlarını korumaktadır. Fakat aynı şey Maxwell denklemleri için geçerli değildir. Maxwell denklemleri Lorentz dönüşümleri altında ancak formlarını koruyabilmektedir. Lorentz dönüşümleri Galile dönüşümlerinden farklı olarak şu şekildedir:
burada  . Lorentz Dönüşümlerinde görüldüğü üzere iki gözlemci için aynı zaman betimlemesi geçerli değildir. Bu dönüşümlerde Einstein'ın Özel Görelilikle ortaya çıkardığı düşünce değişimi görülmektedir, yani farklı hızlardaki iki gözlemci aynı olay için farklı zaman değerleri ölçer.
. Lorentz Dönüşümlerinde görüldüğü üzere iki gözlemci için aynı zaman betimlemesi geçerli değildir. Bu dönüşümlerde Einstein'ın Özel Görelilikle ortaya çıkardığı düşünce değişimi görülmektedir, yani farklı hızlardaki iki gözlemci aynı olay için farklı zaman değerleri ölçer.
Bu dönüşümleri y ve z eksenlerinde de düşünüp yöney (vektör) gösterimi kullanılabilir. Bunun için konumu hıza paralel ve hıza dik olacak şekilde iki bileşene ayırabiliriz:
Bu biçimde sadece hıza paralel olan bileşen olan  dönüşüme uğrar. O hâlde, Lorentz dönüşümleri
dönüşüme uğrar. O hâlde, Lorentz dönüşümleri
biçimine indirgenmiş olur.
Dört boyutlu uzayzaman
- Ana madde: Minkovski uzayzamanı.
Minkovski uzayzamanı, özel göreliliğin dört boyutlu yapısını matematiksel olarak betimleyen geometridir. Bu geometride yöneyler (vektörler) dört bileşene sahiptir. Örneğin Öklid uzayında bir konum yöneyi
olarak ifâde edilir. Özel görelilikte ise "uzayzaman"da bir "konum"u, daha doğru bir deyişle, bir "olay"ı ifâde etmek için dörtyöneyler kullanılır. Bu durumda dörtkonum yöneyi,
-
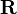
= (ct,x,y,z) 
olarak tanımlanır. Burada dördüncü bileşen olan zamanın ct şeklinde konulması sadece yöneyin her bileşeninin biriminin metre olması içindir. Çoğu kaynak c=1 seçerek daha sâde bir biçim verir. Aynı şekilde dörthız yöneyi de, hızın tanımından
-
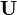


= γ(c,ux,uy,uz) 
olarak çıkarsanır. Buradaks τ özel zamandır.
Aynı şekilde dörtmomentum da,
-

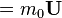
= γm0(c,ux,uy,uz) = (mc,mux,muy,muz) 

olarak bulunur.
Bu uzayzamanda bir dörtyöneyin boyu,
olarak tanılandığından, dörthız yöneyinin boyu
olarak bulunur. Yine, dörtmomentumun boyu
Ayrıca dörtmomentumun boyu
olarak da hesaplanabildiğinden, bu iki sonuç birleştirilip her taraf c2 ile çarpıldığında
gibi özel göreliliğin en önemli denklemlerinden biri elde edilmiş olur.